הסבר על טופולגיית Bus, Star, Ring
טופולוגיות רשת הם כיצד הרשת תיצור קשר עם המכשירים המחוברים אליה, במאמר זה אסביר את סוגי הטופולוגיות הקיימות:
*קודם כדאי לקרוא את מאמר זה, בו אני מסביר על MAU רכזות ונתבים
כל הזכויות שמורות לטל בן שושן – Shushan.co.il
Ring Topology
היא טופולוגיה שכמעט אינה קיימת, היא מהטופולוגיות שהיו קיימות אז בשנות ה-90 וכך מחשבים היו מתקשרים בתוך הרשת ובטופולוגיה זו לא מתרחשים התנגשויות ברשת (להסבר לחצו כאן)
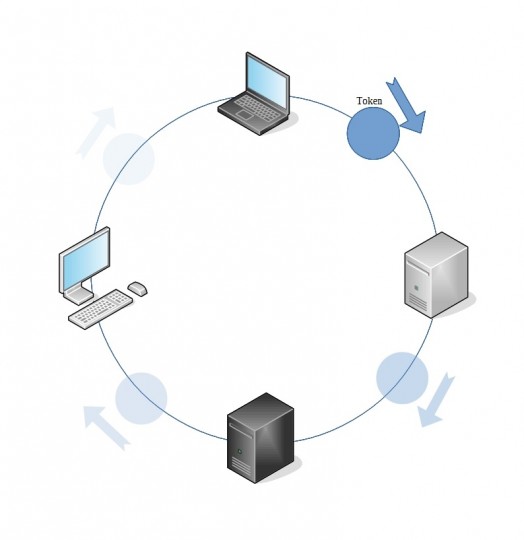
הטופולוגיה הלוגית אומרת שכל המחשבים מחוברים ב Ring "טבעת" ובטבעת היה Token "אסימון" אותו אסימון היה עובר בטבעת בלולאה, ממש כמו בשרטוט.
אותו האסימון היה מכיל את המידע שאחד המחשבים בטבעת נתן לו, זאת אומרת אחד המחשבים היה מחכה שהאסימון יגיע אליו וברגע שהגיע אליו הוא היה בודק אם האסימון ריק ואם הוא ריק היה מכניס לשם את המידע ואת הכתובת למי מיועדת ההודעה
לאחר מכן האסימון היה עובר בטבעת ועובר מחשב מחשב וכל מחשב שהיה מקבל את האסימון היה צריך לבדוק אם המידע שייך לו, ברגע שהאסימון הגיע למחשב המיועד, אותו מחשב היה לוקח את המידע ומשחרר את האסימון בחזרה לטבעת וכך מחשב אחר יכל לשלוח מידע וחוזר חלילה
עכשיו למה אני אומר שזה טופולוגיה לוגית כי טופולגית "כוכב" היא הטופולוגיה הפיזית.
Token Ring
Star Topology
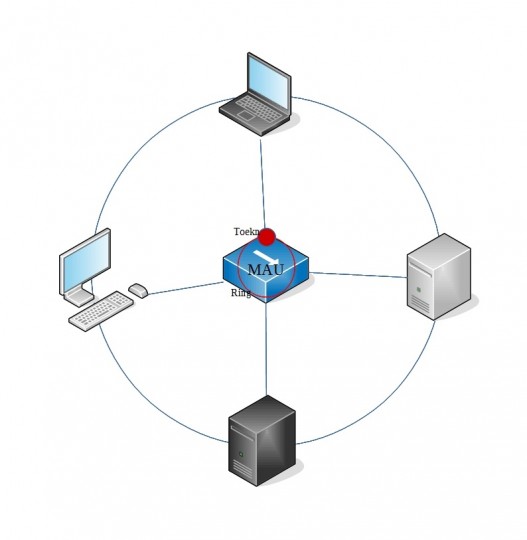
טופולוגיית כוכב היא הטופולוגיה הפיזית (לא רק) של ה Ring Netowork שהסברתי למעלה, אל ה MAU (לחצו כאן להסבר מהו MAU) היו מחוברים את כל המחשבים ממש כמו בשרטוט ה MAU (סוג של רכזת) היה מחבר את המחשבים אליו פיזית ובתוכו היה פועל ה Token Ring ה MAU כאשר היה מקבל מידע היה מעביר את המידע פעם אחת בכל פעם לפורט הבא אחריו וכל פורט שהגיע אם היה מחובר שם מחשב אותו מחשב היה בודק אם ההודעה הייתה מיועדת אליו ואם לא היה מעביר את זה לפורט אחרי וכך לפי הסדר ברגע שאותו מחשב לוקח את המידע הוא משחרר את האסימון וכך האסימון חוזר להיות חופשי והמחשב הבא שרוצה לשלוח מידע בודק את אם האסימון פנוי ואם כן מצוות אליו את המידע ואת המידע למי מיועד וכך חוזר חלילה, האסימון בודק כל פורט אחד אחרי השני (כן כן עובר בפורט 1 ואז עובר לפורט 2 ואז ל3 וכך הלאה).
Star Topology
Bus Topology
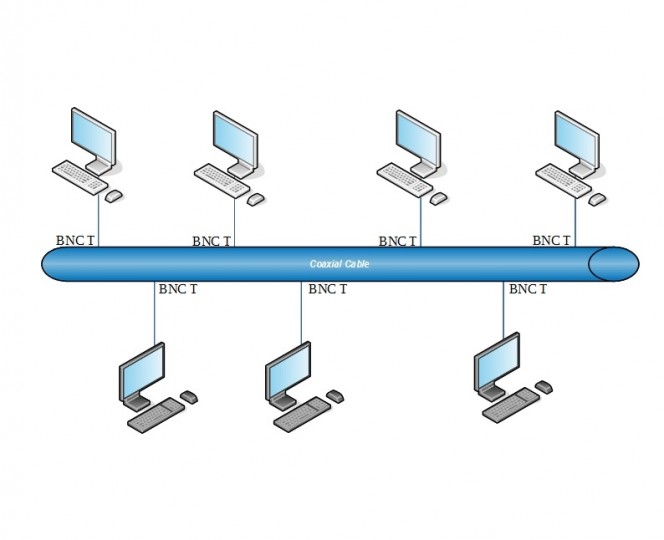
טופולוגיית Bus "אוטובוס" היא טופולוגיה הדומה בצורת הלוגית שלה לאוטובוס ארוך, כל המחשבים היו מחוברים לכבל Coxial ואיתם מחברי BNC בצורת T (ניתן לקרוא כאן על Coxial ועל מחברי BNC) כבל אחד Thinet או Thicknet (גם אותם ניתן לקרוא במאמר שציינתי מקודם) ניקח חדר לדוגמה שבו נמצאים מחשבים ובחדר קיים כבל מסוג Thinet שהוא 10Base2 אליו הכבל הזה היו מחברי BNC בצורת T וכל מחשב נוסף בחדר שהייתם רוצים לחבר הייתם צריכים להוסיף BNC נוסף בצורת T וכך הלאה, הבעיה בצורה זו שפה הייתה מתרחשת התנגשות Collision ובמאמר זה ניתן לקרוא בהרחבה על CSMA\CA ו CSMA\CD שהיו צריכים לחפות על בעיה זו ולמנוע התנגשות.
Bus Topology
Full Mesh Topology
טופולוגית Full Mesh אומרת כך, ניקח חברה מסוימת ולחברה יש את בניין ההנהלה שבו נמצאים כל מנהלי הרשת וחוות השרתים ואותו רוצים לחבר לשאר המשרדים של החברה הנמצאים באזורים גאוגרפיים שונים (WAN) ועל כן יש לחבר את בניין ההנהלה לכל המשרדים וכל המשרדים אחד לשני שעל כן יש בינהם תקשורת וזה מה שאומר טופולוגית Full Mesh, על המשרדים כולל בניין ההנהלה להיות מחוברים אחד לשני וכך משרד יהיה בחיבור ישיר למשרד אחר.
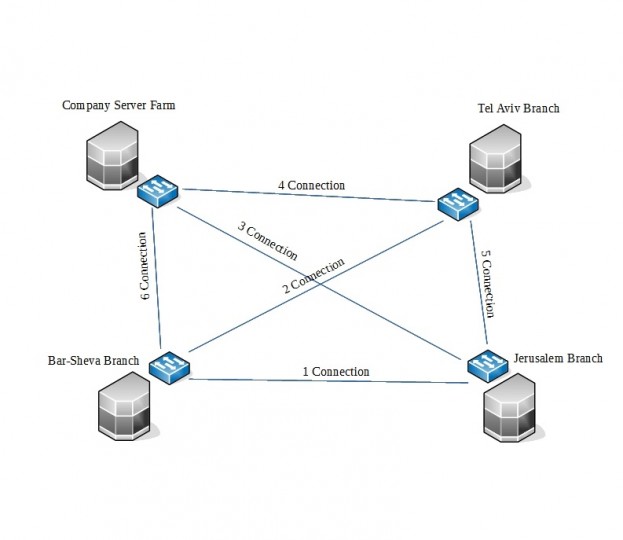
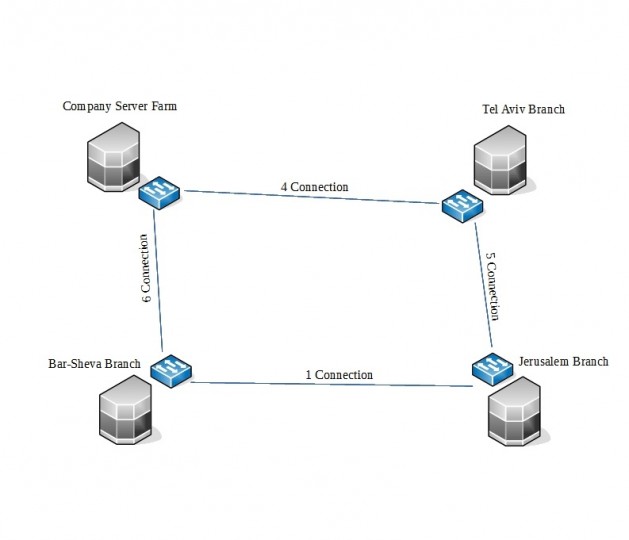
בשרטוט ניתן לראות 4 משרדים האחד הוא הראשי עם חוות השרתים " Company Server Farm" והוא מחובר לסניף תל אביב ואז לסניף ירושלים ואז לסניף באר שבע אבל אם תבחינו תוכלו לראות שב Full Mesh כולם מחוברים לכולם, לכל משרד יש 3 חיבורים יוצאים לשאר המשרדים, ועל כך יש משוואה המשוואה הולכת כך:
Full Meash
N הוא מספר במשרדים שעליכם לחבר, לפי השרטוט שלי יש 4 משרדים שאותם יש לחבר אז אם N= Number of Buildings I need To Connecnt in mesh Toplogy כמות המשרדים שאותם ארצה לחבר בטופולוגיית Mesh ואז אבצע את הנוסחא, התוצאה תיהיה 6 ואם נספור למעלה את כמות החיבורים נגיע לאותה התוצאה
N formula
Hub and Spoke Topology
הוא דומה ל Full Mesh אך הוא חוסך את כמות החיבורים בכך שהוא יוצר חיבור מבניין אחר למשנהו, זאת אומרת ניתן לראות בשרטוט שאם אני רוצה לשלוח הודעה מהמשרדים הראשיים לירושלים אני יכול לעבור דרך תל אביב או דרך באר שבע והכל עדיין יעבוד אבל מה הבעיה בחיבור שכזה, א. החיבור אינו ישיר אלא עובר דרך אחד מהמשרדים מה שעלול לגרום לאיטיות ב. אין לי יתירות ברמת החיבורים ועל כן אם 2 חיבורים יתנתקו אני יאבד גישה אליהם מכל שאר המשרדים
Hub and Spoke Topology
